Class 10 maths CH 6 Triangles DPP
1. In the given figure, if DE || BC, AE = 8 cm, EC = 2 cm and BC = 6 cm, then find DE.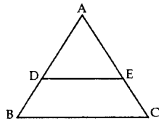
2. In the given figure, XY || QR, PQ/XQ=7/3, and PR = 6.3 cm, find YR.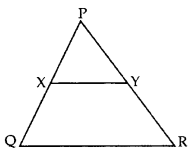
3. The lengths of the diagonals of a rhombus are 24 cm and 32 cm. Calculate the length of the altitude of the rhombus.
4. If ∆ABC ~ ∆PQR, perimeter of ∆ABC = 32 cm, perimeter of ∆PQR = 48 cm and PR = 6 cm, then find the length of AC.
5. If ∆ABC ~ ∆RPQ, AB = 3 cm, BC = 5 cm, AC = 6 cm, RP = 6 cm and PQ = 10, then find QR.
6. ∆ABC ~ ∆DEF. If AB = 4 cm, BC = 3.5 cm, CA = 2.5 cm and DF = 7.5 cm, find the perimeter of ∆DEF.
7. In ∆DEW, AB || EW. If AD = 4 cm, DE = 12 cm and DW = 24 cm, then find the value of DB
8. In ∆ABC, DE || BC, find the value of x.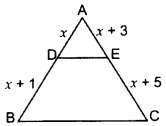
9. The lengths of the diagonals of a rhombus are 24 cm and 32 cm. Calculate the length of the altitude of the rhombus.
10. If PQR is an equilateral triangle and PX ⊥ QR, find the value of PX2
11. In Figure, AB ⊥ BC, FG ⊥ BC, and DE ⊥ AC. Prove that ∆ADE ~ ∆GCF.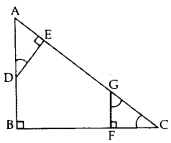
12. In the given figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that ar(ABC)/ar(DBC)=AO/DO. (2012)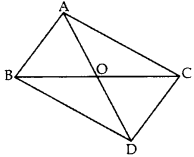
13. Prove that the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.
14. If sides AB, BC and median AD of AABC are proportional to the corresponding sides PQ, QR and median PM of PQR, show that ∆ABC ~ ∆PQR.
15. In the given figure, AD = 3 cm, AE = 5 cm, BD = 4 cm, CE = 4 cm, CF = 2 cm, BF = 2.5 cm, then find the pair of parallel lines and hence their lengths. (2015)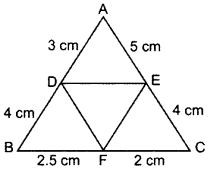
16. In a rectangle ABCD, E is the middle point of AD. If AD = 40 m and AB = 48 m, then find EB.
17. The diagonals of a quadrilateral ABCD intersect each other at the point O such that AOBO=CODO. Show that ABCD is a trapezium.
18. The diagonals of trapezium ABCD intersect each other at point o. If AB = 2CD, find the ratio of area of the ∆AOB to area of ∆COD.
19. ABCD is a rhombus. Prove that AB2 + BC2 + CD2 + DA2 = AC2 + BD2.
20. In ∆ABC, if AP ⊥ BC and AC2 = BC2 – AB2, then prove that PA2 = PB × CP.
21. In the given figure, ∆ABC is right-angled at C and DE ⊥ AB. Prove that ∆ABC ~ ∆ADE and hence find the lengths of AE and DE.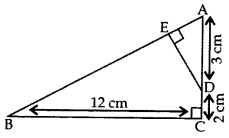
22. In the given figure, AD ⊥ BC and BD = 13CD. Prove that 2AC2 = 2AB2 + BC2. (2012)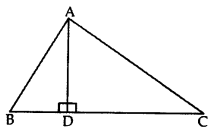
21. In the given figure, the line segment XY is parallel to the side AC of ∆ABC and it divides the triangle into two parts of equal areas. Find the ratio AXAB. (2017OD)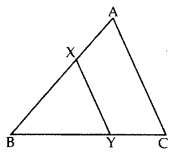
22. In the figure of ∆ABC, D divides CA in the ratio 4 : 3. If DE || BC, then find ar (BCDE) : ar (∆ABC).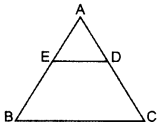
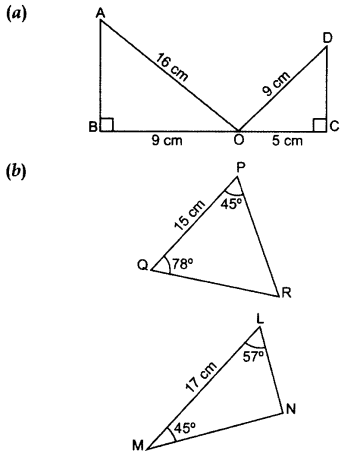
23. State whether the given pairs of triangles are similar or not. In case of similarity mention the criterion.
24. ∆ABC ~ ∆PQR. AD is the median to BC and PM is the median to QR. Prove that AB/PQ=AD/PM.
25. A vertical pole of length 8 m casts a shadow 6 cm long on the ground and at the same time a tower casts a shadow 30 m long. Find the height of tower.