Areas Related To Circle (DPP)
Question 16.
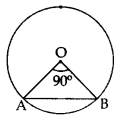
Find the area of the major segment APB, in the figure of a circle of radius 35 cm and ∠AOB = 90°. (Use π =227 ).

Find the area of the major segment APB, in the figure of a circle of radius 35 cm and ∠AOB = 90°. (Use π =
Question 17.
A chord of a circle of radius 14 cm subtends an angle of 120° at the centre. Find the area of the corresponding minor segment of the circle. (Use π =227 and 3–√ = 1.73].
A chord of a circle of radius 14 cm subtends an angle of 120° at the centre. Find the area of the corresponding minor segment of the circle. (Use π =
Question 18.
In Figure, a semi-circle is drawn with O as centre and AB as diameter. Semi-circles are drawn with AO and A OB as diameters. If AB = 28 m, find the perimeter of the shaded region. [Use π =227

In Figure, a semi-circle is drawn with O as centre and AB as diameter. Semi-circles are drawn with AO and A OB as diameters. If AB = 28 m, find the perimeter of the shaded region. [Use π =
Question 19.
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find:
(i) the length of the arc
(ii) area of the sector formed by the arc. [Use π =227 ]
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find:
(i) the length of the arc
(ii) area of the sector formed by the arc. [Use π =
Question 20.
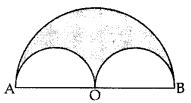
In Figure, two concentric circles with centre O, have radii 21 cm and 42 cm. If ∠AOB = 60°, find the area of the shaded region. (Use π =227 ]

In Figure, two concentric circles with centre O, have radii 21 cm and 42 cm. If ∠AOB = 60°, find the area of the shaded region. (Use π =
Question 21.
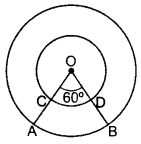
In Figure, APB and AQO are semi-circles, and AO = OB. If the peri-meter of al the figure is 40 cm, find the area of the shaded region. [Use π =227 ]

In Figure, APB and AQO are semi-circles, and AO = OB. If the peri-meter of al the figure is 40 cm, find the area of the shaded region. [Use π =
Question 22.
In Figure, O is the centre of a circle such that diameter AB = 13 cm and AC = 12 cm. BC is joined. Find the area of the shaded region. (Take π = 3.14)

In Figure, O is the centre of a circle such that diameter AB = 13 cm and AC = 12 cm. BC is joined. Find the area of the shaded region. (Take π = 3.14)
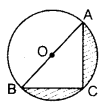
Question 23.
In Figure, are shown two arcs PAQ and 0 PBQuestion Arc PAQ is a part of circle with centre O and radius OP while arc PBQ is a semi-circle drawn on PQ as diameter with centre M. If OP = PQ = 10 cm, show that area of shaded region is 25(3–√=π6 )cm2.

In Figure, are shown two arcs PAQ and 0 PBQuestion Arc PAQ is a part of circle with centre O and radius OP while arc PBQ is a semi-circle drawn on PQ as diameter with centre M. If OP = PQ = 10 cm, show that area of shaded region is 25(
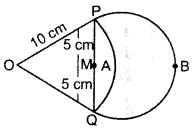
Question 24.
In Figure, O is the centre of the circle with AC = 24 cm, AB = 7 cm and ∠BOD = 90°. Find the area of the shaded region. (Use π = 3.14).

In Figure, O is the centre of the circle with AC = 24 cm, AB = 7 cm and ∠BOD = 90°. Find the area of the shaded region. (Use π = 3.14).
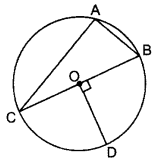
Question 25.
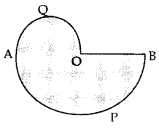
In Fig., AB and CD are two diameters of a circle with centre 0, which are perpendicular to each other. OB is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region. (Use π =227 )

In Fig., AB and CD are two diameters of a circle with centre 0, which are perpendicular to each other. OB is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region. (Use π =
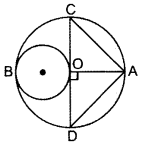
Question 26.
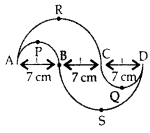
In Figure, APB and CCD are semi-circles of diameter 7 cm each, while ARC and a BSD are semi-circles of diameter 14 cm each. Find the perimeter of the shaded region. [Use π =227 ]

In Figure, APB and CCD are semi-circles of diameter 7 cm each, while ARC and a BSD are semi-circles of diameter 14 cm each. Find the perimeter of the shaded region. [Use π =
Question 27.
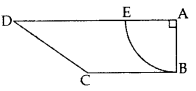
In Figure, ABCD is a trapezium of area 24.5 sq. cm. In it, AD || BC, ∠DAB = 90°, AD = 10 cm and BC = 4 cm. If ABE is a quadrant of a circle, find the area of the shaded region. [Take π =227 ]

In Figure, ABCD is a trapezium of area 24.5 sq. cm. In it, AD || BC, ∠DAB = 90°, AD = 10 cm and BC = 4 cm. If ABE is a quadrant of a circle, find the area of the shaded region. [Take π =
Question 28.
Find the area of the minor segment of a circle of radius 14 cm, when its central angle is 60°. Also find the area of the corresponding major segment. [Use π =227 ]
Find the area of the minor segment of a circle of radius 14 cm, when its central angle is 60°. Also find the area of the corresponding major segment. [Use π =
Question 29.
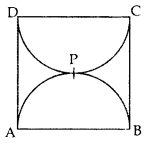
Find the perimeter of the D shaded region in Figure, if ABCD is a square of side 14 cm and APB and CPD are semicircles. [Use π =227 ]

Find the perimeter of the D shaded region in Figure, if ABCD is a square of side 14 cm and APB and CPD are semicircles. [Use π =
Question 30.
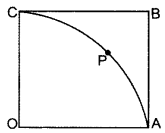
In Figure, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O, then find the area of the sha- o ded region. [Use π =227 ].

In Figure, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O, then find the area of the sha- o ded region. [Use π =
Answers;
