Table Of Trigonometry
Trigonometry is a branch of mathematics that deals with relationships between the sides and angles of triangles and the calculations based on them, particularly right triangles. It includes the study of functions such as sine, cosine, and tangent and their applications to solve problems in fields like physics, engineering, and surveying. The trigonometry table provides you with the values of each function at different angles.
Table of Contents
Why is the Table of trigonometric ratios important?
Tables of trigonometry are important because they provide a quick and easy way to access the values of trigonometric functions for common angles, which saves time and reduces the likelihood of errors when performing calculations. They also serve as a reference for verifying results and can be used to approximate values for angles that are not easily calculated. Additionally, tables of trigonometry are used in various fields such as engineering, physics, and navigation, where the accurate measurement of angles and calculation of trigonometric functions is crucial. These tables are very important for CBSE Board Classes 10,11 and 12.
In this post, we will provide a detailed overview of trigonometry tables, including their history, structure, and learning technique. We will also explore the different types of trigonometry tables, how to use them, and download them. By understanding the fundamentals of trigonometry tables, you can perform complex calculations with ease and accuracy. Whether you’re a student learning about trigonometry for the first time, or a professional in a related field, having a solid understanding of trigonometry tables is essential.
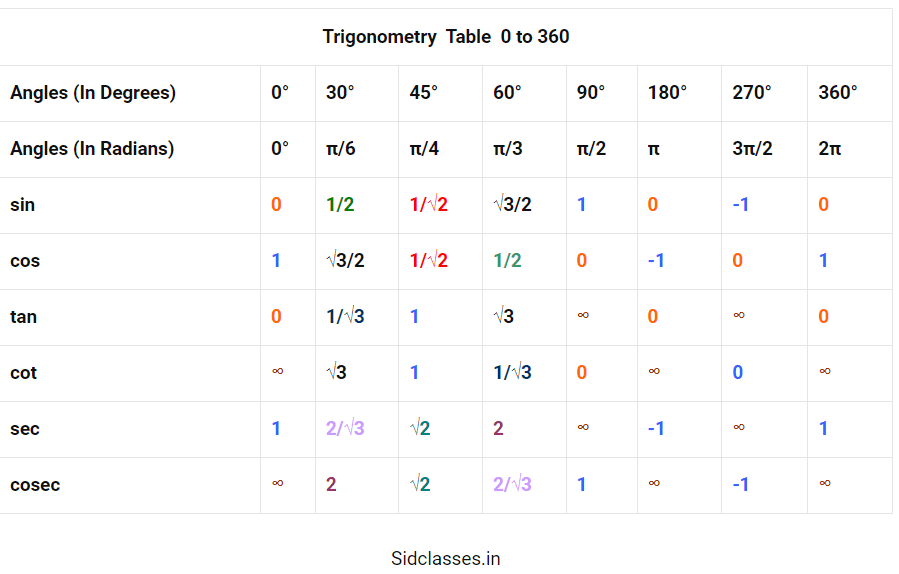
Trigonometry Table (0°-360°)
| Angle in Degrees | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| Angle in Radian | 0 | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
| Sin | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
| Cos | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
| Tan | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
| Cot | ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 0 | ∞ |
| Sec | 1 | 2/√3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
| Cosec | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ |
How to remember the Table of trigonometric ratios?
Many students often find it tough and complicated to learn Trigonometric function values. Here we have tried to put forward some methods that will help you to learn these values. However, if you know the formulas of Trigonometry then it will be much easier to learn these formulas.
Below are some trigonometry formulas based on angles.
- sin x = cos (90° – x)
- cos x = sin (90° – x)
- tan x = cot (90° – x)
- cot x = tan (90° – x)
- sec x = cosec (90° – x)
- cosec x = sec (90° – x)
Below are some formulas based on reciprocals.
- 1/sin x = cosec x
- 1/cos x = sec x
- 1/tan x = cot x
- 1/cot x = tan x
- 1/sec x = cos x
- 1/cosec x = sin x
How to learn the values of Sin x?
Well to determine the values of sin x, you can divide 0, 2, 3, and 4 by 4 and then find their square roots. [sin 0° = √0/4 = 0] , [Sin 30° = √2/4 = 1/2] etc.
Or directly remember the values of sin.
How to learn the values of Cos x?
To determine the values of cos x, you can divide 4, 3, 2, 1, 0 by 4 (opposite in sequence as sin x ) and then find their square roots. [cos 0° = √4/4 = 1] , [cos 30° = √3/4 = √3/2] etc.
How to learn the values of tan x?
To determine the values of tan x, you can divide sin x by cos x. As tan x = sin x/ cos x
How to learn the values of Cot x?
The value of Cot x is reciprocal of tan x, simple.
How to learn the values of Sec x?
The value of sec x is reciprocal of cos x, simple.
How to learn the values of Cosec x?
The value of cosec x is reciprocal of sin x, simple.
About Table of trigonometry
Trigonometry is a branch of mathematics that focuses on the study of the relationships between the angles and sides of triangles. It is used in various fields such as physics, engineering, architecture, and astronomy, among others.
The three primary functions in trigonometry are sine, cosine, and tangent. These functions relate the ratios of the sides of a right triangle to the angles opposite them. The sine function (sin) represents the ratio of the length of the side opposite an angle to the length of the hypotenuse. The cosine function (cos) represents the ratio of the length of the adjacent side to the length of the hypotenuse. The tangent function (tan) represents the ratio of the length of the opposite side to the length of the adjacent side.
Trigonometry also involves inverse functions such as arcsine, arccosine, and arctangent. These functions enable one to determine the value of an angle given the ratio of the sides of a triangle.
Trigonometry has many practical applications, such as calculating the height of buildings, determining the angle of a satellite dish, or calculating the distance between two points on a map. It is also used in more advanced areas of mathematics such as calculus and differential equations.
What is a Table of Trigonometry?
A trigonometry table is a reference tool that lists the values of the six trigonometric functions (sine, cosine, tangent, cosecant, secant, and cotangent) for specific angles. It typically presents angles in degrees or radians and provides the corresponding values of these functions. Trigonometry tables are a vital aid in solving complex trigonometric equations, verifying trigonometric identities, and simplifying calculations in physics and engineering.
How to Read the Table of trigonometry?
Although a trigonometry table may seem intimidating, it is relatively straightforward to read. The table has columns representing the six trigonometric functions and rows representing angles in degrees or radians. To use the table, locate the row that corresponds to the angle you are working with and read across the row to find the values of the six trigonometric functions for that angle. For instance, if you are working with a 30-degree angle, find the row that corresponds to 30 degrees, and then read across to find the sine, cosine, tangent, cosecant, secant, and cotangent of that angle.
Advantages of Using a Table of trigonometric ratios
Using a trigonometry table has numerous advantages that make it an indispensable tool for anyone working with trigonometry. Some of these benefits include:
Saves time: Instead of calculating the values of trigonometric functions manually, a trigonometry table allows you to look them up quickly and accurately for specific angles, thus saving you time.
Increases accuracy: Trigonometry tables provide accurate values of trigonometric functions, helping to reduce errors in calculations.
Simplifies calculations: Trigonometry tables simplify complex calculations in fields such as physics, engineering, and navigation, making it easier to obtain accurate results.
Downloadable Table of trigonometric ratios PDF
To make things even more accessible, we have created a downloadable trigonometry table PDF that you can use for reference. Our PDF includes the values of the six trigonometric functions for angles ranging from 0 to 360 degrees in increments of 5 degrees, as well as values of the functions for angles in radians. By downloading our PDF, you will have a comprehensive reference tool at your fingertips for all your trigonometry needs.
The Structure of Trigonometry Tables
Trigonometry tables are structured in a specific way to make it easy to locate and use the values of the different trigonometric functions. Typically, the table is divided into two parts: the angle column and the function column. The angle column lists the different angles in degrees, while the function column lists the corresponding values of the trigonometric function for each angle.
For example, if we look at the sine function in a trigonometry table, we can see that the value of sin 30° is 0.5. Similarly, the value of sin 45° is √2/2. The table makes it easy to find the value of any trigonometric function for a given angle.
The History of Trigonometry Tables
Trigonometry tables have a rich history that dates back to the ancient civilizations of Egypt, Greece, and India. The earliest trigonometry tables were developed by the Greek mathematician Hipparchus in the 2nd century BC. These tables contained values for the sine and cosine functions for angles ranging from 0 to 180 degrees.
Over the years, trigonometry tables have undergone various transformations, including the addition of new functions such as tangent, cotangent, secant, and cosecant. Today, trigonometry tables are widely available in both print and digital formats and are used in a wide range of fields, including navigation, astronomy, and surveying.
We hope that the above Trigonometry table helped you a lot, If you have any queries regarding the same topic, you can ask us in the comment section. For more such content please visit Sid Classes again.
Learn Trigonometry with RS Aggarwal Class 12 Book – Click Here to view a pdf of the full book